关于随着喷丸时间的增加,阿尔门试片的弧高值的增加越来越小的现象可以公式 h=r.σh.t 得到量化,由此公式可以得出:
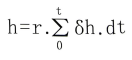
希腊字母∑表示总和-即在0到t的时间段里,每一小时间段 dt中δh的总和。在时间t中对阿尔门试片进行喷丸是积分学的一个应用!阿尔门试片的弧高值就是在已知时间段中大量的凹坑作用总和的结果。
任何形状的曲线都可以用相对应的公式表达出来。对于喷丸强度曲线我们可以用许多的公式来表达。一个“首近似值”的曲线形状表达公式是双参数的指数方程,如下式所示:(1)
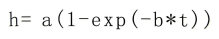
其中,a和b是双参数。
如果我们对上面的方程进行微分,即可以得到小凹坑对阿尔门试片弧高值的贡献情况:(2)
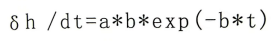
6上述方程就是“凹坑贡献曲线”,也就是说单个的凹坑对阿尔门试片弧高值的贡献δh随喷丸时间的变化情况。下图显示了基于方程(1)的喷丸强度曲线以及基于方程(2)的对应凹坑贡献曲线。从图中可以清楚地看出随着喷丸时间的增加,额外的喷丸对弧高值增加的贡献非常迅速地下降到了一个很小的值。
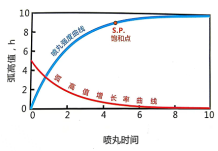
下表罗列出了四个大家比较熟悉的公式来拟合喷丸强度曲线,并列出了相对应的微分方程,即凹坑贡献曲线。
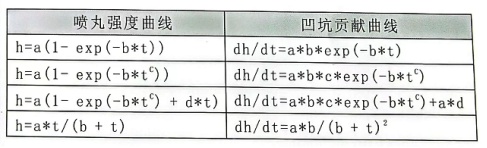
如果我们采用双参数方程来拟合喷丸强度曲线,那么其中的一个参数b反映了凹坑的生成速率,另一个参数a反映了这些凹坑对于弧高值的贡献。因为关于凹坑对弧高值的贡献只有一个参数,因此关于弧高值形成的机械影响因素也只有一个,那就是表面的塑性变形。上述公式也反映出了随着喷丸时间的增加,凹坑对弧高值的贡献也在不断下降。我们都知道,三参数和四参数公式对于饱和曲线的已知形状的表达会更加准确。额外多的参数可以表示弧高值生成的其它机械因素。