我们来谈一谈测具测试吧~ 每一个测试得到的弧高值h均是大量的个体的σh累计而得到的,这和雨量器有相似的的特征。下图显示了雨量器的测试方法。
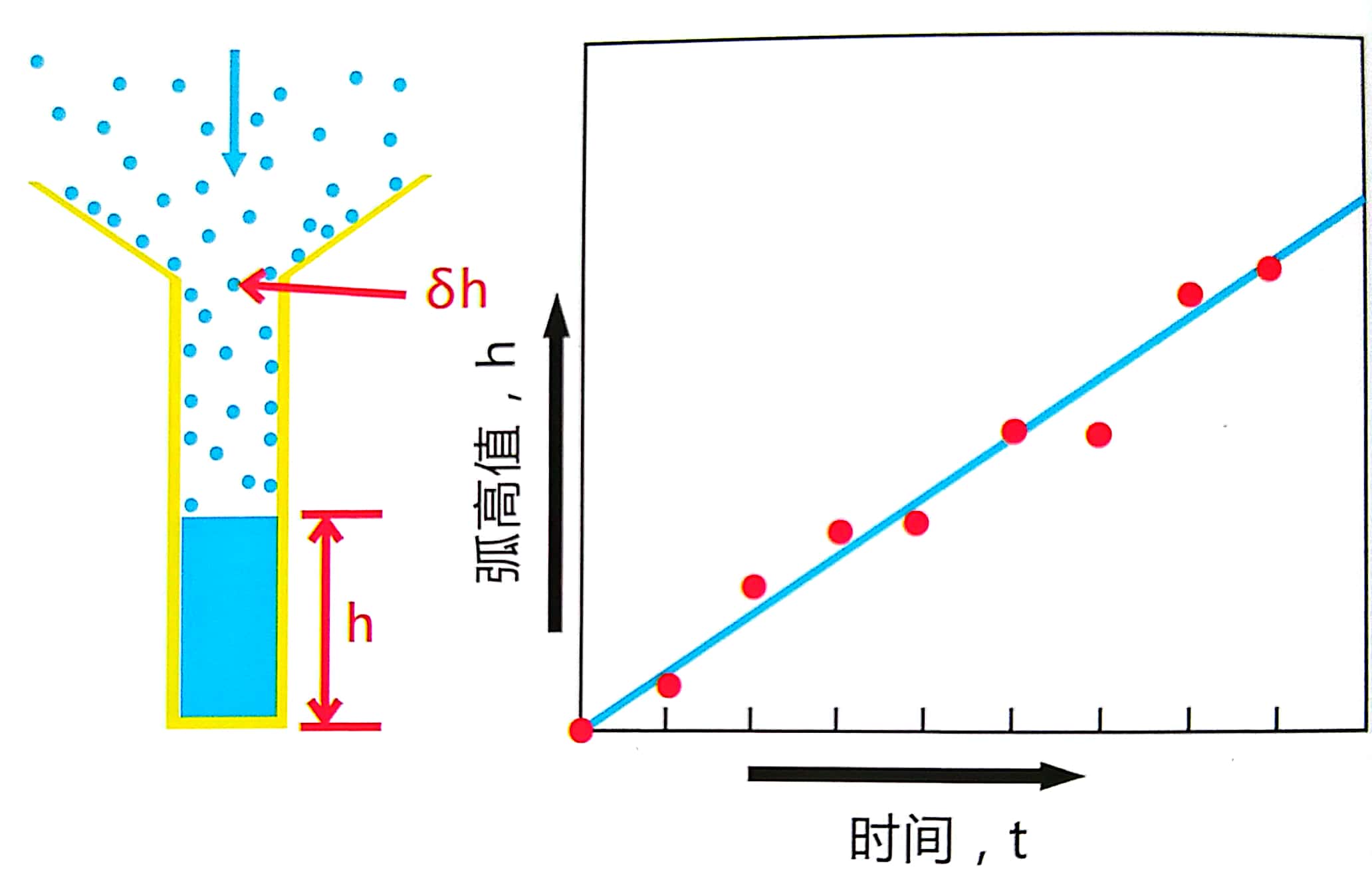
经过一段时间t的收集,雨水的高度为h,每一个雨滴对高度的贡献为σh。雨水斗高度同样受到雨滴进入雨量器的速度的影响。因此可得以下公示:
h=r.σh.t
如果r和σh为已知常量,那么上面的公示可以写成:
h=a.t
其中a是常数。(a=r.σh)
公式 h=a.t 是一哥 直线方程。直线方程可以通过测试不同时间t的高度h而获得,如上图所示。该测试具有统计变化性,因此仅能作为已知公示的参考。在1805年,勒让德发明了“最小二乘法”,可以对现有数据进行最佳拟合,使其符合现有的公式。到了计算机时代,工程师们厌倦了采用手动的方法对试验结果进行最佳拟合。
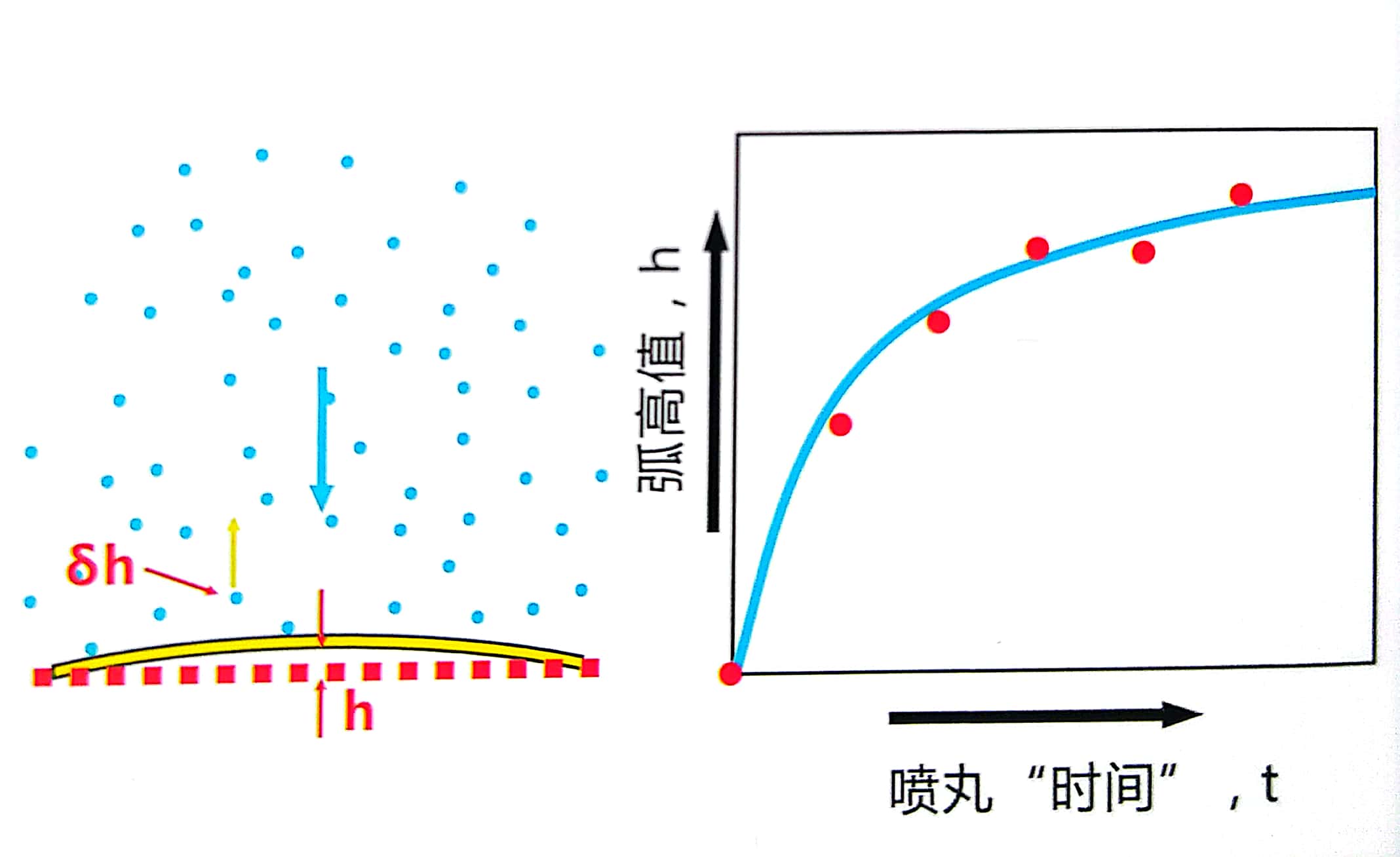
上图和下图采用的类似的方法,显示了阿尔门试片弧高实际值以及其拟合曲线的方法。每一个丸料撞击阿尔门试片表面后均会会产生微量的塑性变形进而产生σh的阿尔门试片弯曲变形量。下图右侧的实际值和拟合已知方程的曲线。
上图和下图的明显差异是其拟合曲线的形状不同。随着喷丸时间的增加,阿尔门试片的弯曲变形σh在不断减小。